Trigonometri: Konsep, Rumus, dan Penerapannya dalam Kehidupan Sehari-hari -Trigonometri merupakan cabang ilmu matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam sebuah segitiga. Istilah ini berasal dari bahasa Yunani, yaitu “trigonon” yang berarti tiga sudut dan “metron” yang berarti mengukur. Trigonometri memiliki peran yang sangat luas, tidak hanya dalam matematika murni, tetapi juga dalam berbagai bidang ilmu dan teknologi.
Konsep Dasar Trigonometri
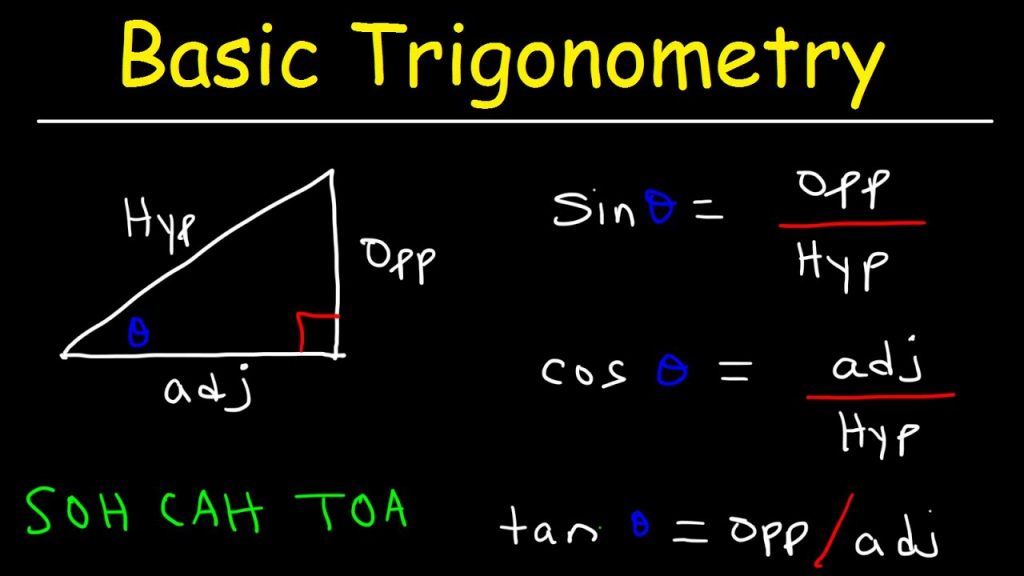
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam sebuah segitiga. Dalam segitiga siku-siku, terdapat tiga fungsi utama:
1. Sinus (sin θ)
Sinus dari suatu sudut adalah perbandingan antara panjang sisi yang berhadapan dengan sudut tersebut terhadap panjang sisi miring.
Rumus: sin θ = sisi depan / sisi miring
2. Kosinus (cos θ)
Kosinus dari suatu sudut adalah perbandingan antara panjang sisi yang berdekatan dengan sudut tersebut terhadap panjang sisi miring.
Rumus: cos θ = sisi samping / sisi miring
3. Tangen (tan θ)
Tangen dari suatu sudut adalah perbandingan antara panjang sisi yang berhadapan dengan sudut tersebut terhadap panjang sisi yang berdekatan.
Rumus: tan θ = sisi depan / sisi samping
Identitas Trigonometri
1. Identitas Pythagoras
sin² θ + cos² θ = 1
1 + tan² θ = sec² θ
1 + cot² θ = csc² θ
2. Identitas Perbandingan
tan θ = sin θ / cos θ
cot θ = cos θ / sin θ
3. Identitas Kebalikan
sin θ = 1 / csc θ
cos θ = 1 / sec θ
tan θ = 1 / cot θ
Penerapan Trigonometri dalam Kehidupan Sehari-hari
1. Mengukur Ketinggian Bangunan
Dengan menggunakan sudut elevasi dan panjang bayangan, tinggi suatu bangunan dapat dihitung tanpa perlu mengukurnya langsung.
2. Navigasi Maritim dan Udara
Trigonometri digunakan untuk menghitung posisi kapal atau pesawat berdasarkan sudut dan jarak terhadap titik acuan tertentu.
3. Astronomi dan Eksplorasi Luar Angkasa
Trigonometri berperan penting dalam perhitungan jarak antara planet dan bintang.
4. Teknik Sipil dan Arsitektur
Trigonometri digunakan untuk menghitung kemiringan atap dan elemen struktural lainnya dalam bangunan.
5. Teknologi dan Grafika Komputer
Trigonometri digunakan dalam pembuatan animasi, grafik 3D, dan pemrograman simulasi fisika.
Contoh Soal Trigonometri dan Penyelesaiannya
1. Menentukan Panjang Sisi Segitiga
Jika segitiga memiliki sudut 45° dan sisi miring 10 cm, berapa panjang sisi yang berhadapan dengan sudut tersebut?
Penyelesaian:
sin 45° = sisi depan / 10
0.707 = sisi depan / 10
sisi depan = 10 × 0.707 = 7.07 cm
2. Menentukan Sudut dari Perbandingan Sisi
Sebuah tangga memiliki panjang 5 meter dengan jarak dasar ke dinding 4 meter. Tentukan sudut antara tangga dan tanah.
Penyelesaian:
cos θ = 4 / 5
θ = cos⁻¹ (0.8)
θ ≈ 36.87°
Kesimpulan
Trigonometri memiliki banyak aplikasi dalam kehidupan sehari-hari, termasuk dalam pengukuran bangunan, navigasi, astronomi, dan teknologi. Pemahaman yang baik tentang trigonometri sangat berguna dalam berbagai bidang ilmu dan profesi.